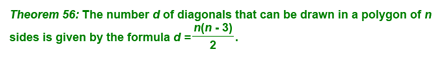Printable version

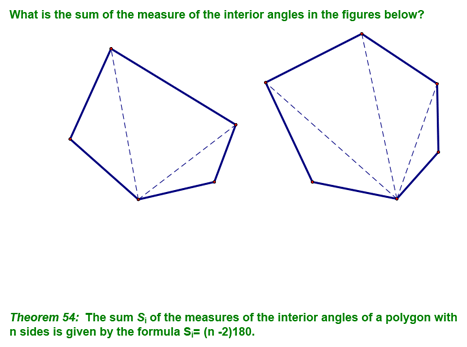
Formulas Involving Polygons - Lesson 7-3

Today, started by learning how polygons are classified by their number of sides...you already knew a lot of these - just make sure to memorize the ones you don't know!!

Next, we looked at the diagonals of polygons with different numbers of sides. We realized that by drawing as many diagonals as we could from one diagonal, that we could see a pattern...we can make n-2 triangles in a n-sided polygon. Given this information and the fact that the sum of the interior angles of a polygon is 180°, we came up with the following theorem:

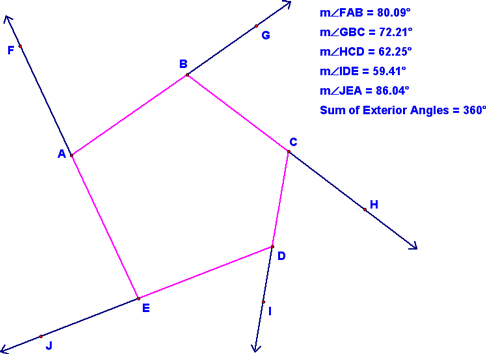
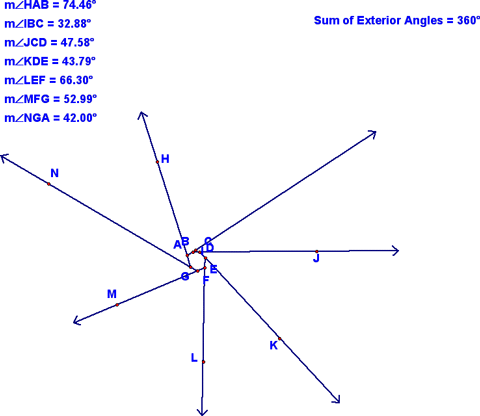
After that, we looked at exterior angles in a polygon. First, we looked at the exterior angles of a pentagon as shown below:

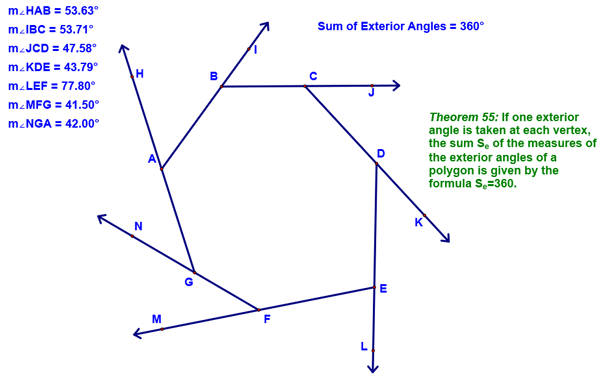
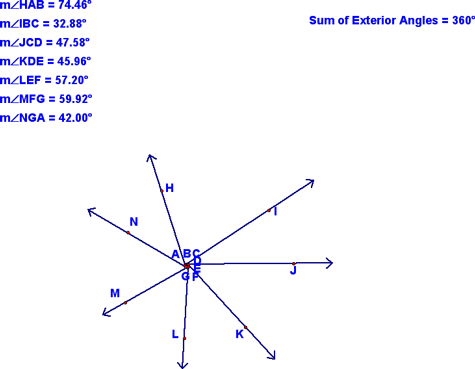
Note that the sum of the exterior angles is 360°. Remember that I moved the sides of the pentagon around, thereby changing the measure of the exterior angles, but that the sum always stayed 360°. Next, we looked at a heptagon and found the same to be true. In fact, this is true of all polygons and can be written as a conjecture:

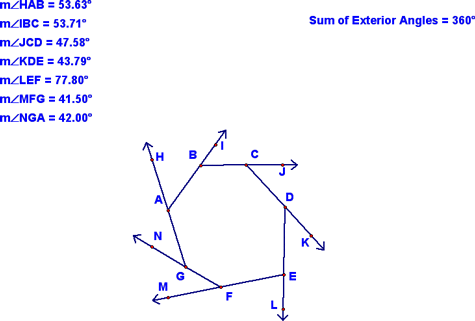
Also remember the dilation I showed you...I shrunk down the heptagon, keeping the angles the same measure. This showed that the exterior angles formed a circle (therefore must sum to 360°. If you don't understand the following sequence of images, don't sweat it...just remember that the sum of the exterior angles is 360° no matter how many sides the polygon has:

We then reviewed the following theorem...I showed some of you the derivation of this, but am not holding you responsible for it!